Abstract
- 무엇이 Deep 네트워크에서 일반화(generalization)을 이끄는가?
- 저자들은 당시에 제안된 설명들을 분석하고 각각의 평가 Measure들이 얼마나 일반화를 보장할 수 있는지를 측정함.
Introduction
- over parameterized 세팅에서는 여러개의 global minima가 생길 수 있다. 그런 경우는 여러 global minima들 모두 training error는 최소화 되지만 그 중 다수는 generalize가 잘 되지 않는다. → Training Error를 최소화하는 것은 일반화를 보증하지 못함
- optimizer의 변경, BatchSize 등이 일반화에 영향을 미치는 경우가 존재하기 때문에 파라미터의 숫자나 모델의 아키텍쳐만 가지고 도출되는 measure는 일반화를 설명하기에 불충분함.
- 어떤 것들이 Neural Network에서 일반화를 보장할 수 있을까?
- complexity나 capacity control은 뭐랑 관련된 걸까?
- norm이나 margin-based measure가 주로 capacity control에 사용됨
- sharpness (파라미터의 변화에 training error가 robust한 정도)나 PAC-Bayes 분석기법이 complexity measure로 제안됨
딥러닝에서 일반화를 설명할 수 있는 complexity measure는 무엇이 필요한가?
- 일반화를 보장하기에 충분해야 함
- 실제로 해당 measure 아래 학습했을 때, complexity가 낮아야 함
- 기존 uniform measure(모델 파라미터 수 등)로 설명되지 않는 아래의 현상들을 설명할 수 있어야 함
- 실제 레이블을 가지고 학습한 일반화가 잘된 모델과 같은 아키텍쳐로 랜덤 레이블을 학습해도 training error를 0까지 떨어뜨릴 수 있음. 우리는 해당 measure에서 실제 label로 학습한 모델의 complexity가 랜덤 레이블를 학습한 모델보다 낮기를 기대함.
- 모델의 파라미터를 키웠을 때 training error는 차이가 없지만 실제 일반화의 성능은 증가하는 경우가 있음. 해당 measure 상으로 모델의 파라미터가 커지면 complexity가 줄어들기를 기대함
- optimization 방법(optimizer or initial parameter)만 다르고 똑같은 구조와 데이터셋으로 학습을 시켰을 때, 양쪽 모두 training error는 0이지만 한쪽이 더 일반화가 잘되는 경우가 있음. 해당 measure가 이런 실제 일반화 성능과 상관관계를 갖기를 기대함.
- 저자들은 당시에 제안된 complexity measure들(norm, robustness, sharpness 등)이 일반화를 잘 설명하는지 여부를 이론적, 실증적으로 검증함
Notation
\(f_{\mathbf{w}}(\mathbf{x})\): function computed by a \(d\) layer feed-forward with parameter \(\mathbf{w}\) and ReLU
\(f_{\mathbf{w}}(\mathbf{x})=\mathbf{\textit{W}}_d\phi(\mathbf{\textit{W}}_{d-1}\phi(...\phi(\mathbf{\textit{W}_1}\mathbf{x})))\)* where *\(\phi(z)=\max\{0,z\}\)
\(\textit{D}_i^{\mathbf{x,w}}\): \(i\) 레이어에서 activation함수에 대응되는 대각 {1,0} 행렬. 단순화를 위해 위에쓴 \(\mathbf{x}\)를 지우고 \(\textit{D}_i\)로 씀.
\(f_{\mathbf{w}}(\mathbf{x}) = W_dD_{d-1}W_{d-1}\cdots D_1W_1\mathbf{x} = W_d(\Pi_{i=1}^{d-1}D_iW_i)\mathbf{x}\).
\(h_i\): \(i\) 레이어에서 노드의 개수, \(h_0=n\)
모든 레이어 \(i\)에 대해, \(W_i \in R^{h_i\times h_{i-1}}\)
\(\ell(\mathbf{w,x})\): input이 \(x\)일 때, 함수 \(f_\mathbf{w}\)의 예측에 의한 Loss
\(L(\mathbf{w})\): 예상되는 loss
\(\widehat{L}(\mathbf{w})\): 트레이닝 셋에 대해 학습했을 때 경험적 loss
\([k]: \{1,2,\cdots,k\}\) (임의의 정수 \(k\)에 대해)
\(\|\cdot\|_F\): Frobenius norm
\(\|\cdot\|_2\): spectral norm
\(\|\cdot\|_1\): element-wise \(\ell_1\)-norm
\(\|\cdot\|_\infty\): element-wise \(\ell_\infty\)-norm
Generalization and Capacity Control in Deep Learning
-
저자들은 일반화를 보장하기 위해 요구되는 example의 개수 측면에서 capacity를 고려함
→ 그 숫자는 거의 “랜덤 레이블로 학습했을 때 충분히 작은 training error까지 도달할 수 있는 example의 최대 개수”에 대응됨
어떤 feedforward나 convolution으로 표현되는 모든 함수의 집합인 모델 클래스 \(\mathcal{H}\)가 주어졌을 때, 어떤 complexity measure를 다음의 맵핑 \(\mathcal{M}\)으로 볼 수 있다.
\(\mathcal{M}:\{\mathcal{H,S}\} \rightarrow \mathbb{R} ^+\), \(\mathcal{S}\) 는 학습셋
이때 제한된 클래스 \(\mathcal{H}_{\mathcal{M},\alpha}=\{h:h\in \mathcal{H},\mathcal{M}\leq\alpha\}\)를 생각할 수 있다. (\(\alpha\geq0)\)
그러면 \(\mathcal{H}_{\mathcal{M,M}(h)}\)의 capacity 관점에서 학습된 가설 모델 \(h\) 는 일반화가 되었다고 보증할 수 있다.
\(\mathcal{M}(h)\)의 값이 더 작은 \(h\)가 더 잘 일반화 되었을 것이라고 기대한다.
Network Size
- 어떤 모델이든 유한한 정확도의 파라미터를 가지고 있다. 모델의 capacity는 파라미터의 수에 비례한다. Bartlett과 Harvey는 feedforward 네트워크의 VC 차원을 아래와 같이 타이트하게 범위를 구했다.
→ 파라미터의 숫자가 샘플의 숫자보다 많은 over-parameterized 세팅에서는 파라미터 수에만 의존하는 measure는 너무 약하고 모델의 일반화를 설명할 수 없음
- 요즘 실제 활용되는 모델들은 샘플보다 많은 파라미터를 가진 경우가 많으며, 일반화되지 않고 랜덤 레이블조차 완벽하게 학습함.
Norms and Margins
- capacity는 파라미터의 숫자와 상관없이 \(\ell_2\) norm regularized 등으로 통제될 수 있다.
예를 들어 capacity는 각 레이어의 hidden unit의 \(\ell_1\)norm에 기반해 경계가 그어질 수 있다. 그건 \(\Pi_{i=1}^d\|W_i\|_{1,\infty}^2\) 에 비례한다. 여기서 \(\|W_i\|_{1,\infty}\)는 레이어 i의 hidden unit의 \(\ell_1\)norm중에서 최대값을 뜻한다.
\(\ell_{p,q}\): 각 hidden unit의 \(\ell_p\)norm 값들의 \(\ell_q\)norm 이다.
예를 들어 \(\ell_{2,2}\)는 \(\ell_F\)(=\(\ell_2)\)norm과 같다.
\(\ell_p\) path norm: \(\Pi_{i=1}^d\|W_i\|_{p,\infty}\)
\(\ell_p\) path norm은 node-wise rescaling에도 값이 변하지 않는다는 장점이 있다.
node-wise rescaling: \(W_i\)에 \(\alpha\)를 곱하고 \(W_{j}\)에 \(\frac1\alpha\)를 곱해줘 scailing을 재분배하는 것
만약 zero/one loss를 사용한다면(틀린개수 세기) loss는 전체 weight값을 반으로 줄이거나 두 배로 늘려도 달라지지 않음. (맞고 틀리고는 똑같을 테니) 따라서 임의의 아주 작은 norm을 얻을 수 있게 됨. ce-loss처럼 scale sensitive한 loss함수를 사용하면 이 문제를 해결할 수 있음.
하지만, ce-loss를 사용하면 loss를 계속 줄이기 위해 결과값이 infinity로 커지는 문제가 발생함. 그러면 weight의 norm도 infinity로 커짐. 결국 이때 norm 값은 언제 멈추었냐의 정도의 의미가 된다.
→ 결국 다른 optimization method나 hyper parameter로 학습한 모델을 weight의 norm으로 비교하는 것은 의미가 없음
대신 다른 network간 Norm의 비교를 유의미하게 만드는 방법은 network output의 scailing을 포함하는 것.
margin: \(f_{\mathbf{w}}(\mathbf{x})[y_{true}]- \max_{y \ne y_{true}} f_{\mathbf{w}}(\mathbf{x})[y]\)
(\(x\): single data point)
정답 레이블의 값과 정답이 아닌 레이블의 값 중 가장 큰 값의 차이를 margin으로 사용한다. 여러 입력데이터가 있을 때 가장 작은 값을 사용하는 건 예외적인 입력에 민감하기 때문에 margin 값은 하위 \(\epsilon\) 비율에 해당하는 데이터의 margin을 사용한다. 이때의 margin을 \(\gamma_{margin}\)이라고 한다. \(\epsilon\)은 0.001 에서 0.1사이가 적절.
margin을 이용해 capacity에 비례하도록 보정한 결과는 다음과 같다.
\(\ell_2\) norm → \(\frac1 {\gamma_{margin}^2}\Pi_{i=1}^d 4\|W_i\|_F^2\)
\(\ell_1\)-path norm → \(\frac1{\gamma_{margin}^2} (\Sigma_{j \in \Pi_{k=0}^d [h_k]} |\Pi_{i=1}^d 2W_i[j_i,j_{i-1}]|)^2\)
\(\ell_2\)-path norm → \(\frac1{\gamma_{margin}^2} \Sigma_{j \in \Pi_{k=0}^d [h_k]}\Pi_{i=1}^d 4h_iW_i^2[j_i,j_{i-1}]\)
spectral norm → \(\frac1{\gamma_{margin}^2} \Pi_{i=1}^d h_i\|W_i\|_2^2\)
이 식들은 parameter 수와 독립적으로 norm의 측면에서 capacity의 경계를 설정할 수 있다.
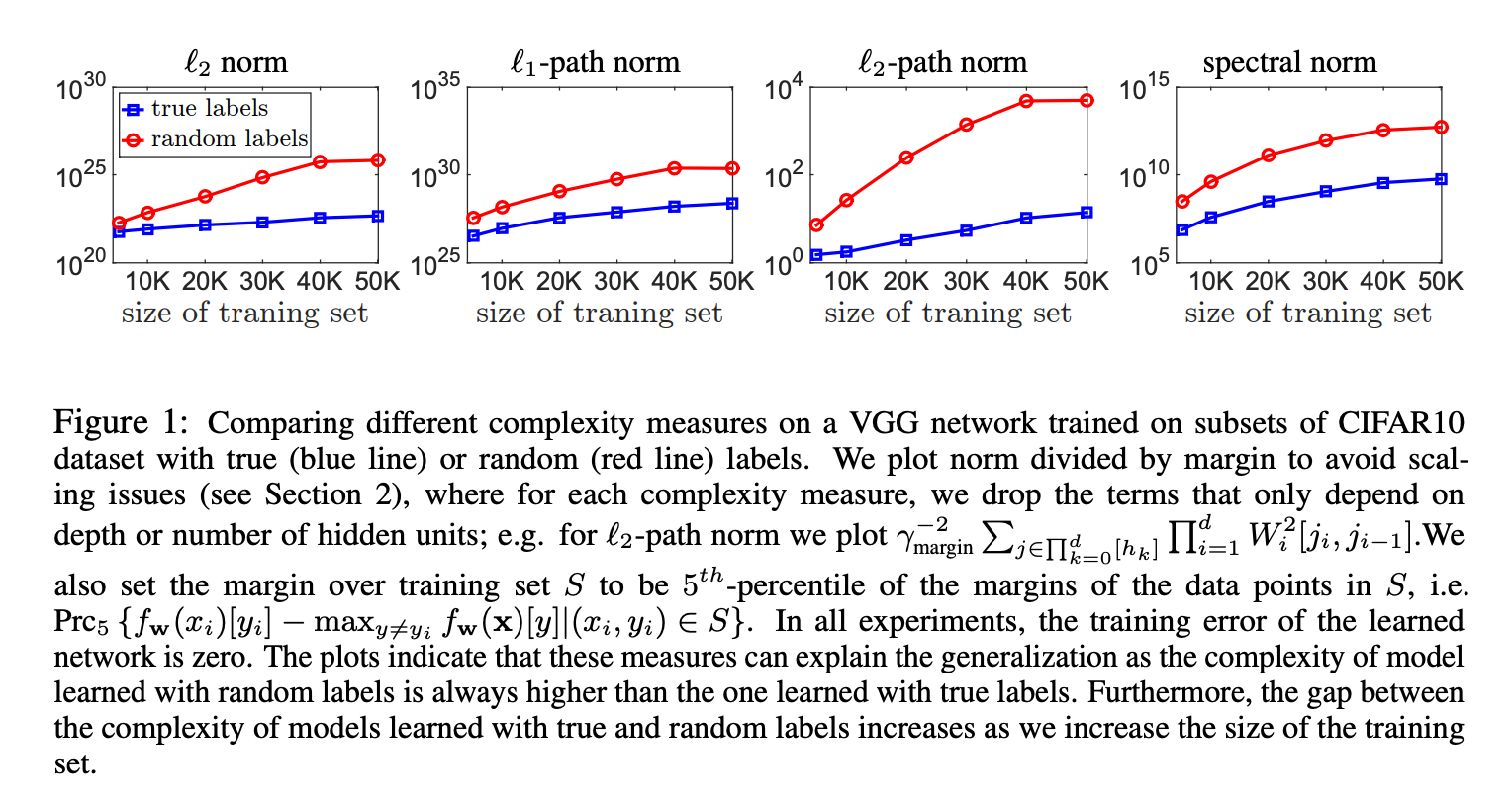
저자들은 norm을 실제 레이블과 랜덤레이블로 학습했을 때를 비교했다. 저자들이 기대한 것은 두 가지이다.
- 실제 레이블로 학습했을 때, 랜덤레이블로 학습한 모델보다 complexity가 낮을 것
- 랜덤 레이블을 학습했을 때, capacity가 training 샘플의 수에 비례해 증가하는 것, 그 증가폭이 실제 레이블일 때 보다 더 클 것. (랜덤 레이블을 학습시키려면 모든 추가적인 샘플은 새 capacity를 필요로하기 때문)
결과는 실제로 그렇게 나왔다.
Lipschitz Continuity and Robustness
- 립시츠 상수로 capacity의 경계를 설정할 수 있을까?
- 일반화를 설명할 때 립시츠 상수 자체만으로 충분한가?
capacity control를 립시츠 연속 측면에서 다룸.
\(\mathcal{X}\): input space, \(\mathcal{M}\): metric(거리 함수) 일때
\(f : \mathcal{X} \rightarrow \mathbb{R}\) on metric space \((\mathcal{X}, \mathcal{M})\)
\(|f(x)-f(y)| \leq C_{\mathcal{M}}\mathcal{M}(x,y)\) 를 만족하는 \(C_{\mathcal{M}}\)이 존재할 때 \(f\)는 립시츠 함수이다.
- \(f\)는 모델에 대응되고 \(\mathcal{M}\)은 input space \(\mathcal{X}\)에서의 distance function에 대응된다
Luxburg and Bousquet는 metric space \((\chi, \mathcal{M})\)에서 립시츠 상수와 유한한 diam로 경계를 정할 수 있는 함수들의 capacity를 연구했다.
\[diam_{\mathcal{M}}(\mathcal{X}) = \sup_{x,y \in X} \mathcal{M}(x,y)\]그들은 \((\frac{C_{\mathcal{M}}}{\gamma_{margin}})^n diam_{\mathcal{M}}(\mathcal{X})\) 에 비례하는 capacity를 제시했지만 이 capacity bound는 input size에 지수적 의존성을 갖는다는 약점이 있다. (n이 뭔지가 안나와있는데 정황 상 input dimension이 n으로 보임)
관련된 또 다른 접근 중에는 robustness가 있다.
\(\epsilon>0\)인 \(\epsilon\)이 주어졌을 때, \(\mathcal{X}\)를 아래의 조건을 만족하는 \(K\)개의 disjoint 집합으로 partioning할 수 있다면, 학습된 모델 \(f_{\mathbf{w}}\)는 \(K\)만큼 robust하다.
트레이닝 셋 \(\mathbf{s}\)에 있는 모든 \((\mathbf{x}, y)\)에 대해 각각의 disjoint set \(C_i\)은 다음을 만족한다.
\[\mathbf{x,z} \in C_i \Rightarrow |\ell(\mathbf{w,x})-\ell(\mathbf{w,z})| \le \epsilon\]이때 \(K\) robust한 모델의 capacity는 \(K\)이다.
\(K\)는 \(C_{\|\cdot\|}\)로 설명할 수 있는데, 이 때 립시츠 \(C_{\|\cdot\|}\)나 \(C_{\ell_\infty}, C_{\ell_2}\) 립시츠 상수를 사용하면 결과적으로 input dimension과 네트워크 depth에 지수적인 의존성을 갖게된다.
→ 결국 립시츠 상수만으로는 capacity conrol을 합리적으로 설명할 수 없다.
Sharpness
sharpness라는 파라미터 space에 대한 적대적 변동에 robust한지를 측정하는 개념이 일반화의 측정도구로 당시에 제시되었다.
\[\zeta_\alpha(\mathbf{w}) = \frac{\max_{|\nu_i| \le \alpha(|\mathbf{w}_i|+1)}\widehat{L}(f_\mathbf{w+\nu})-\widehat{L}(f_\mathbf{w})}{1 + \widehat{L}(f_\mathbf{w})} \simeq \max_{|\nu_i|\le \alpha(|\mathbf{w}_i|+1)} \widehat{L}(f_\mathbf{w+\nu})-\widehat{L}(f_\mathbf{w})\]여기서 \(\widehat{L}(f_\mathbf{w})\)는 보통 neural net에서 매우 작기 때문에 중요하지 않은 것으로 보아 sharpness를 제시한 저자들은 단순하게 분모를 무시했다.
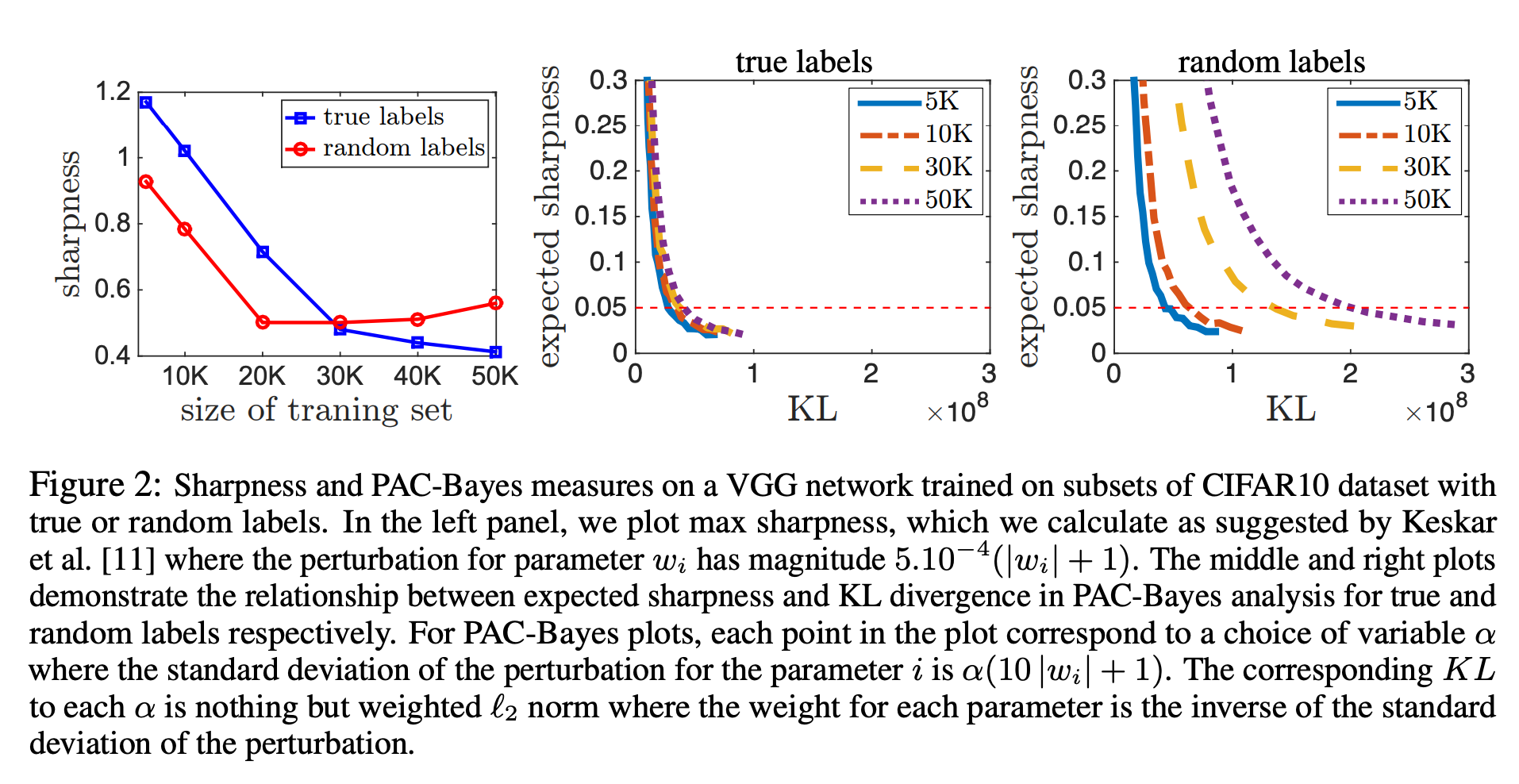
하지만 sharpness는 모델의 일반화를 측정할 수 없다.
- 첫째로 랜덤 라벨로 학습한 모델과 실제 라벨로 학습한 모델을 보면 가장 왼쪽 그림인 sharpness는 모델의 크기가 클 때는 맞게 표현되었지만 모델의 크기가 작을 때는 오히려 random label의 sharpness가 더 떨어졌다.
- 게다가 sharpness는 \(\mathbf{w}\)의 스케일에 의존성이 있기 때문에 파라미터의 스케일을 조정해 인위적으로 크거나 작게 만들 수 있다.
→ sharpness는 모델의 capacity를 컨트롤하기에 충분하지 않다.
대신에 저자들은 expected sharpness를 PAC Bayesian 프레임워크의 맥락으로 보는 관점을 옹호했다.
sharpness와 norm을 함께 사용함으로써 capacity control를 제공하며, 많은 관측된 현상을 설명할 수 있다.
PAC Bayesian 분석은 \(\mathcal{Q}\)라는 학습 데이터에 의존적인 분포(때때로 posterior 불리는)에서 랜덤하게 뽑힌 predictor (hypothesis)의 기대되는 에러의 범위를 보장한다.
\(f_\mathbf{w}\): 학습 데이터로 학습된 어떤 예측 함수
\(\mathbf{w}\): 학습 데이터로 학습한 predictor
\(\nu\): 확률 변수
predictor에 대한 분포 \(\mathcal{Q}\)를 \(\mathbf{w}+\mathbf{\nu}\)로 나타낼 수 있다.
학습데이터와는 독립적인 가설에 대한 prior 분포 \(P\)가 주어졌을 때, \(f_{\mathbf{w}+\nu}\)는 다음과 같다. (Simplified PAC-Bayesian Margin Bounds)
\(\mathbb{E}_\nu[L(f_\mathbf{w+\nu})] \le \mathbb{E}_\nu[\widehat{L}(f_\mathbf{w+\nu})] + \sqrt{\mathbb{E}_\nu[\widehat{L}(f_\mathbf{w+\nu})]\mathcal{K}}+\mathcal{K}\), where \(\mathcal{K}=\frac{2(KL(\mathbf{w}+\nu\|P) + \ln\frac{2m}{\sigma})}{m-1}\)
neuralnet에서는 training Loss \(\mathbb{E}_\nu[\widehat{L}(f_\mathbf{w}+\nu)]\)가 \(\mathcal{K}\)보다 작을 때가 많으므로, 뒤쪽 항이 중요하다.
위 식을 조정하면 weaker bound로 다음 식을 얻을 수 있다.
\[\mathbb{E}_\nu[L(f_{\mathbf{w}+\nu})] \le \mathbb{E}_\nu[\widehat{L}(f_\mathbf{w+\nu})] + 4 \sqrt{\frac{(KL(\mathbf{w}+\nu\|P)+\ln\frac{2m}{\sigma}}{m}}\]이 식은 아래와 같이 다시 표현할 수 있다.
\[\mathbb{E}_\nu[L(f_\mathbf{w+\nu})] \le \widehat{L}(f_\mathbf{w}) + \underbrace{\mathbb{E}_\nu[\widehat{L}(f_\mathbf{w+\nu})] - \widehat{L}(f_\mathbf{w})}_{\textmd{expected sharpness}} + 4 \sqrt{\frac1m \bigg(KL(\mathbf{w+\nu}\|P)+\ln \frac{2m}{\sigma}\bigg)}\]보시다시피 PAC-Bayes bound는 두 개의 의존성이 있다.
- expected sharpness
- prior P에 대한 KL divergence
이 bound는 어떠한 분포 \(P\), \(\nu\) 그리고 어떤 \(\mathbf{w}\)를 골라을 때도 성립하기 때문에 간단하게 \(P\)를 평균 0, \(\sigma^2\)의 분산인 정규분포로 정의하고 \(\nu\)또한 평균 0에 분산이 \(\sigma^2\)인 spherical 가우시안으로 선택하면 다음 식이 된다.
\[\mathbb{E}_\nu[L(f_\mathbf{w+\nu})] \le \widehat{L}(f_\mathbf{w}) + \underbrace{\mathbb{E}_\nu[\widehat{L}(f_\mathbf{w+\nu})] - \widehat{L}(f_\mathbf{w})}_{\textmd{expected sharpness}} + 4 \sqrt{\frac1m \bigg(\underbrace{\frac{\|\mathbf{w}\|_2^2}{2\sigma^2}}_{\textmd{KL}} +\ln \frac{2m}{\sigma}\bigg)}\]- 위의 일반화는 capacity control을 expected sharpness와 norm을 함께 활용하여 명확한 방법으로 설명한다.
- 앞에서 sharpness자체는 스케일을 고려하지 않는다고 했는데 위의 bound에서는 norm과 sharpness가 \(\sigma\)를 통해 직접적으로 상호작용한다. (norm을 키우기 위해 \(\sigma\)를 줄이면 sharpness가 같이 작아지고, 반대도 마찬가지) 그러므로 합리적인 bound를 얻기 위해서는 \(\sigma\)를 적절히 선택해야 한다.
- 저자들은 실험을 통해 위의 meaure가 일반화의 오류를 더 잘 표현한다는 것을 관찰했다. (위의 Figure 2에서도 그렇게 나타남)
Empirical Investigation
저자들은 앞서 말한 measure들이 정말로 효과적인지를 검증하는 실험을 진행했다.
Difference Global Minima
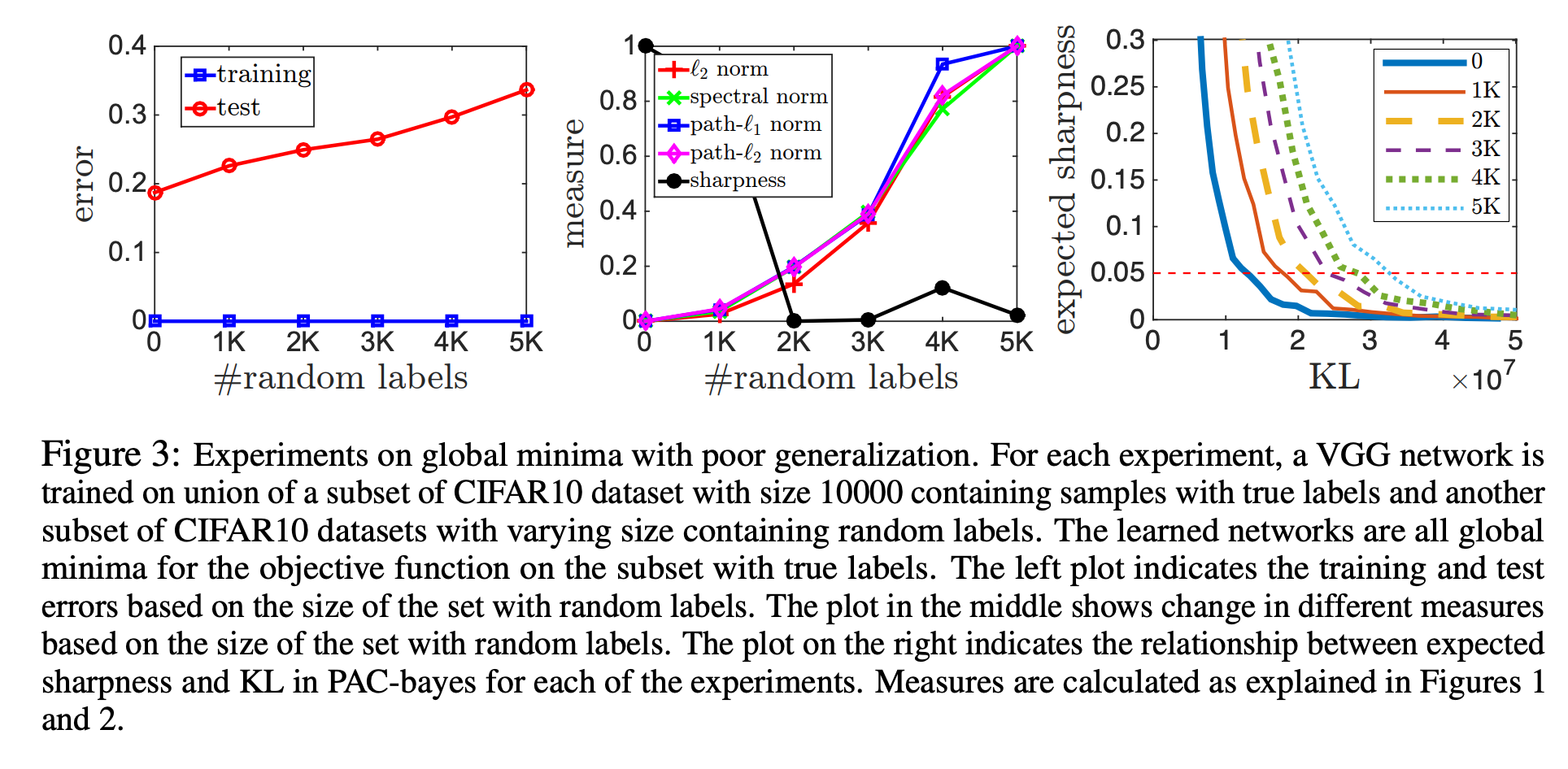
여러 방법으로 objective function에 대한 global minima에 도달한 모델들을 어떻게 비교할까?
- 저자들은 CIFAR 10에서 진짜 label 10000개에 랜덤 label을 개수를 달리해 추가적으로 학습시키면서 각각이 다른 global minima에 도달하도록 했다.
- 앞에서 예상한 대로 norm 기반의 접근은 좋은 지표를 보였으며, sharpness는 잘 동작하지 않았다. PAC-Bayes measure 또한 잘 예측했다.
Increasing Network Size
MNIST 데이터셋을 이용해 모델의 크기에 따라 measure들이 영향을 받는 모습을 실험했다.
- 저자들은 sensible compexity measure라면 test error의 양상처럼 모델 크기가 커짐에 따라 예측 값이 작아지기를 기대했다.
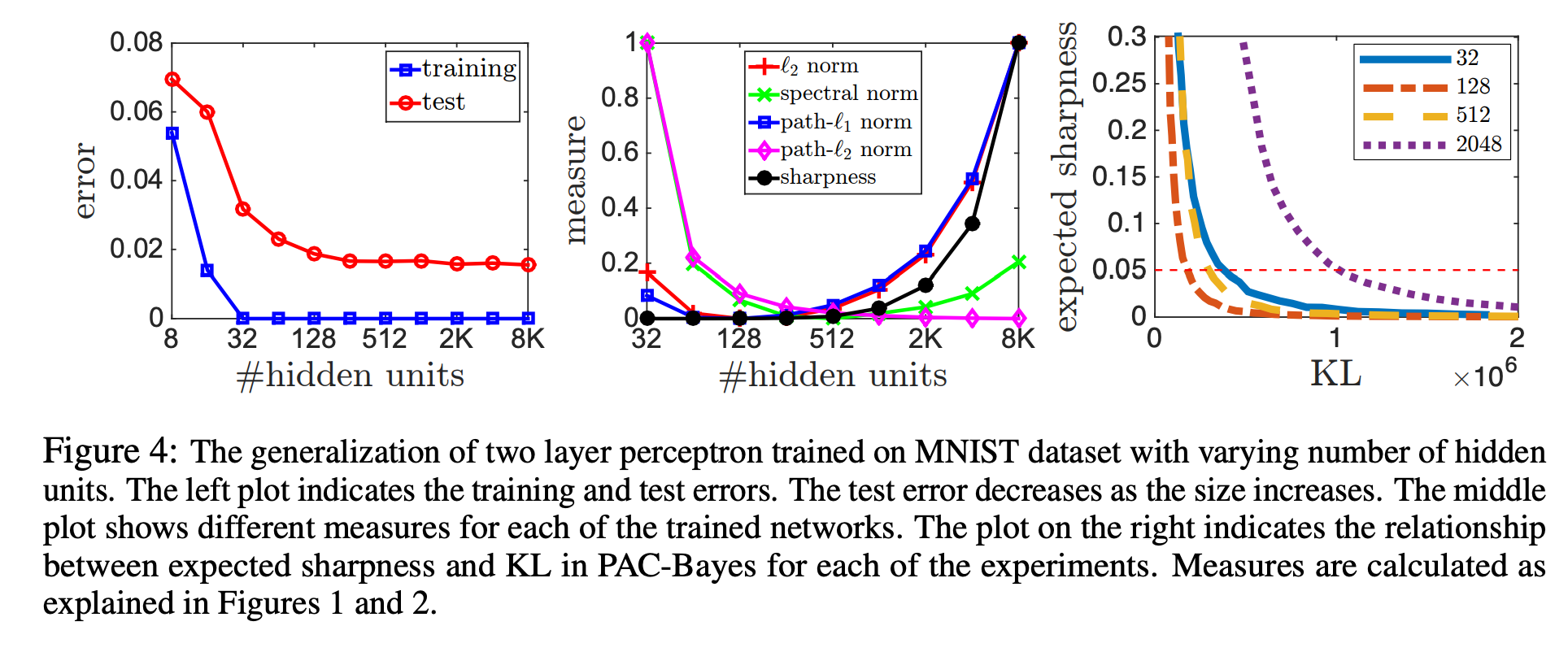
- norm 기반의 접근은 hidden unit이 128까지는 유효한 예측을 했지만 norm은 앞서 말한 대로 hidden unit의 개수에 의존성이 있기 때문에 그 이후는 제대로 예측하지 못했다.
- expected sharpness의 경우에도 128까지는 제대로 예측했지만 그 보다 더 큰 네트워크의 일반화를 제대로 설명하지 못했다.
- 이 점은 neuralnet에서 발견되는 모든 일반화 현상을 설명하기에는 아직 부족하다는 점을 시사한다.
Conclusion
- 딥러닝에서는 실제로 잘 동작하는 많은 일반화 현상이 아직 잘 설명되지 않고 있다.
- 이 논문에서는 일반화 현상을 설명하는 여러 complexity measure의 후보군을 살펴보고 비교했다.
- 아직도 마땅한 선택지는 없지만 expected sharpness와 norm의 조합은 neural network의 일반화 현상을 훨씬 더 잘 설명하는 것으로 보인다.