• ∞-former: Infinite Memory Transformer

Abstract

• 바닐라 트랜스포머를 제한이 없는 장기기억을 이용해 확장한 ∞-former를 제안
• ∞-former의 attentention complexity는 context 길이와 독립적이며 memory 크기와 정확도 간의 트레이드오프가 있음
• sorting, language modeling, dilaogue generation 등의 task로 실험해서 성능을 검증

Introduction

• ∞-former는 트랜스포머에 unbounded long-term memory(LTM)으로 확장시켜 임의 길이의 context에 어텐션을 적용할 수 있도록 함.
• LTM의 키 아이디어는 연속적인 공간 상의 어텐션으로 모델의 입력이 \(N\)개의 radial basis function의 선형조합인 연속된 신호로 표현됨.
• 이렇게하여 ∞-former의 어텐션 complexity는 바닐라 트랜스포머의 \(\mathcal{O}(L \times (L+L_{\text{LTM}}))\)과 달리 \(\mathcal{O}(L^2 + L \times N)\)
• 덕분에 토큰의 수보다 작은 \(N\)을 설정하여 연산량을 줄일 수 있고 항상 임의의 길이의 context를 고정된 크기로 표현할 수 있음

• 물론 계산량이 줄어든 만큼 정확도에서 손실을 보는 문제가 나타내는데 이 문제를 해결하기 위해 sticky memory를 도입. 자주 사용되는 기억에 더 큰 공간을 할당하여 중요한 정보는 영구적으로 기억될 수 있도록 함

• 저자들이 말하는 기여점
  • ∞-former를 제안해 입력의 길이와 어텐션의 복잡도를 독립적으로 만들어 긴 context를 다룰 수 있게 만듬
  • 모델이 메모리에 제한이 없는 context를 유지하는 방법을 제시
  • 중요한 정보가 오래 보존되도록 강제하는 sticky memory 도입
  • 3종류의 task에 대해 실험적으로 비교하고 이점을 보여줌

Background

\(L\): 입력의 길이

\(e\): Embedding의 크기

\(X= [x_1, \ldots, x_L ] \in \mathbb{R}^{L \times e}\) : 입력 시퀀스

\(Q, K, V\): 어텐션의 Query, Key, Value

Continuous Attention

• 2020년에 제안된 Continuous attention 메커니즘은 단어에 대한 어텐션 확률 질량 함수를 신호에 대한 확률 밀도 함수로 대체
• continuous attention을 사용하기 위해 먼저 \(X \in \mathbb{R}^{L \times e}\) text 입력을 연속된 신호로 변환
  • 이는 입력을 basis function의 조합으로 표현하는 것
• 각 \(x_i\ (i\in \{1, \ldots, L \})\) 마다 시간 사이의 위치 \(t_i \in [0,1]\)로 맵핑됨. \(t_i = i / L\)
• 그러면 모든 \(t \in [0,1]\)에 대해 연속 공간 표현 \(\bar{X}(t) \in \mathbb{R}^e\)을 얻을 수 있음

\[\bar{X}(t) = B^\intercal \psi(t)\]

• \(\psi(t) \in \mathbb{R}^N\)는 \(N\)개의 RBF의 벡터

• \(B\)는 multivariate ridge regression으로 얻을 수 있음

• 입력을 연속된 신호 \(\bar{X}(t)\)로 변환한 뒤 다음은 이 신호에 대해 어텐션을 하는 것.
• 일반 어텐션 처럼 입력에 대해 discrete한 확률 분포를 사용하지 않고 확률 밀도 \(p\)를 사용함.

\[c = \mathbb{E}_p [\bar{X}(t)]\]

Infinite Memory Transformer

• 저자들은 바닐라 트랜스포머에 연속적인 LTM을 이용해 긴 context를 활용할 수 있도록 함
• LTM은 이전 스텝의 입력 임베딩과 hidden state를 저장하고 있음
• 뿐만 아니라 TransformerXL에서 했던 것처럼 hidden state를 확장하는 short-term memory (STM)의 활용가능성도 고려

Long-term Memory

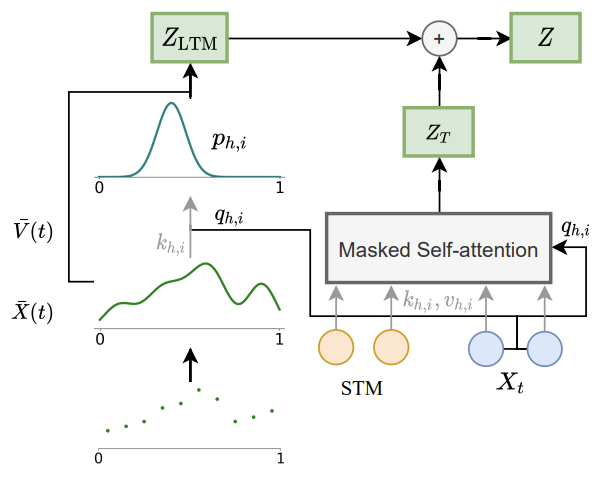
• infinity-former에서 각 레이어의 결과 \(Z\)는 TransformerXL에서 처럼 입력과 hidden state cache로 얻는 \(Z_T\)와 장기기억으로 얻는 \(Z_{LTM}\)을 더해서 얻음
• \(\bar{X}(t)=B^\intercal \psi(t)\) 에서 \(B\)를 각각 linear 레이어로 projection해서 \(K, V\)를 얻고 \(K\)로부터 평균과 분산을 구해서 확률밀도 함수 \(p\)를 얻고, \(V\)에 \(\psi\)함수를 곱해 다시 value signal을 얻은 뒤 \(p\)를 가중치로 \(V\)와 가중합 하여 \(Z_{LTM}\)을 얻음.

Unbounded Memory

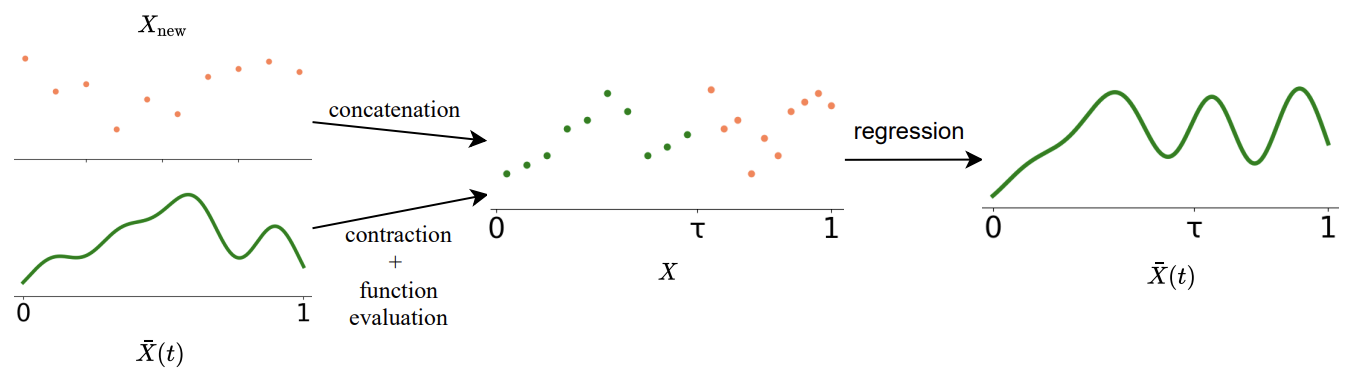
• 이산적인 sequence를 기억으로 사용하면 확장하기 위해 새 hidden state를 저장해야 함.
• \(\infty\)-former는 고정된 크기에 무제한의 context를 기록할 수 있음.
  1. 먼저 \(\bar{X}(t)\)에서 \([0,1]\) 사이의 \(M\)개의 위치를 샘플링
  2. 그리고 그 점들에 새로운 점들을 \(\tau\)를 기준으로 앞 뒤로 이어 붙임.
  3. 이 점들을 이용해 다시 multivariate ridge regression을 이용해 새 \(\bar{X}(t)\)를 얻음.

Sticky Memories

• LTM에서 \([0,1]\) 사이의 \(M\)개의 위치를 샘플링할 때, 일정한 간격으로 샘플링을 할 수 있지만 그러면 사실 특정 위치가 다른 위치보다 더 중요할 수 있음을 고려하지 못함.
• 저자들은 \(M\)개의 위치를 각각의 영역에서의 연관성을 이용해 샘플링하는 방법을 제안
  1. 먼저 신호 구간을 \(D\)개의 영역으로 일정하게 나눔

  2. 그리고 각 영역마다 확률을 계산함 (\(H\)는 head의 개수, \(L\)은 sequence length)

     \[p(d_j) \propto \sum_{h=1}^H \sum_{i=1}^L \int_{d_j} \mathcal{N}(t; \mu_{h,i}, \sigma_{h,i}^2)\ dt\]
  3. 그리고 각 영역마다 확률 값에 따라서 총 \(M\) 개의 위치를 샘플링

Experiments

Sorting

• 임의의 순서로 주어진 숫자 입력을 내림차순으로 정렬해서 생성하는 task
• TransformerXL, Compressive Transformer를 baseline 삼아 비교

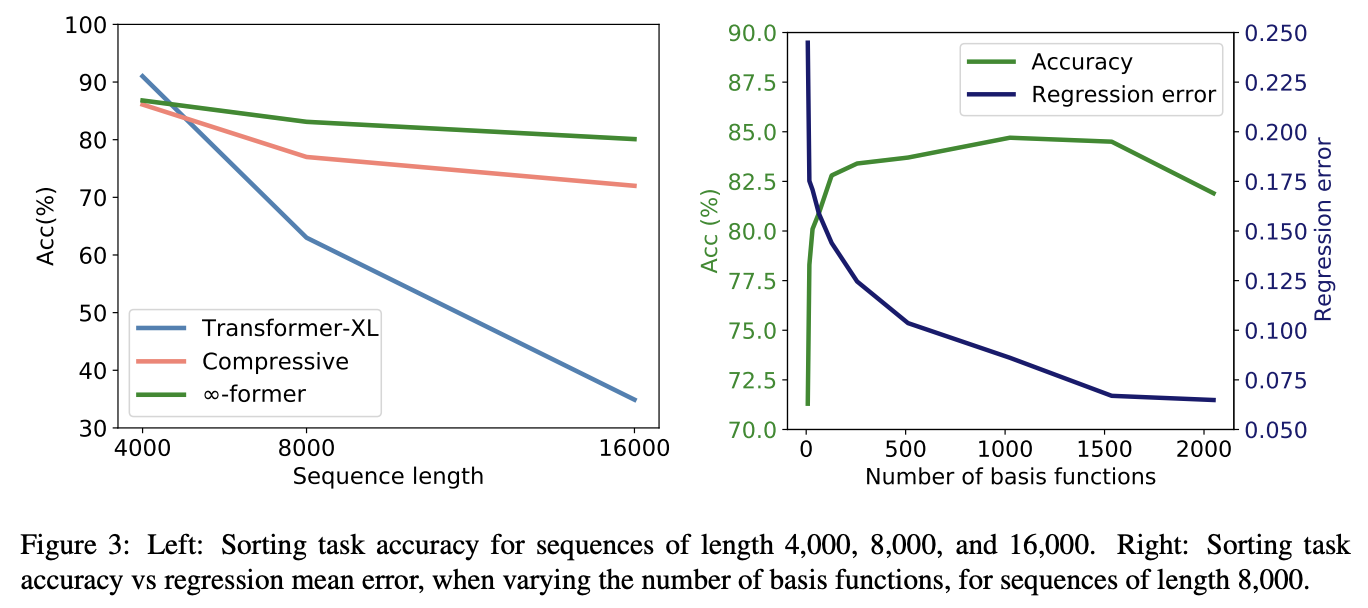
• 모델의 크기나 메모리의 크기는 공평하게 설정
• sequence length가 짧을 때는 Transformer-XL은 모든 정보를 메모리에 기억하고 있어 가장 성능이 좋지만 길어지면 성능이 크게 하락함
• compressive transformer보다 성능이 좋음

Language Modeling & Document Grounded Dialogue

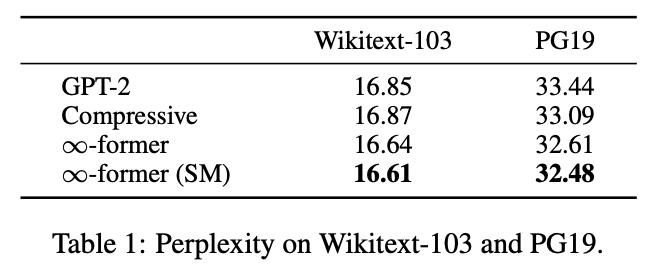
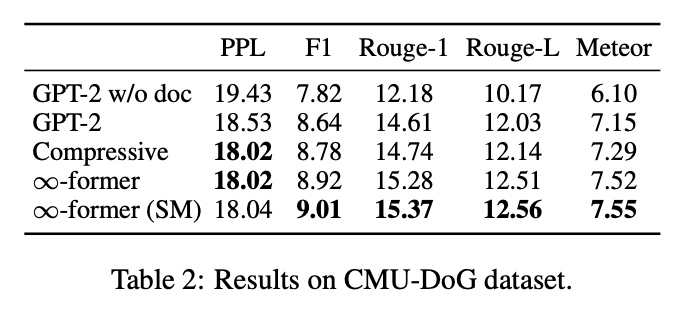
• \(\infty\)-former가 가장 좋았다.
• 더 긴 context에 대한 기억이 필요한 PG-19에서 Wikitext-103 보다 성능차가 컸다.
• Sticky Memory를 쓰는 게 더 좋았다.

Conclusions

• 무제한의 장기기억을 활용할 수 있는 \(\infty\)-former 모델을 제안
• 연속된 공간 상의 어텐션을 사용하여 입력의 길이와 독립적인 attention complexity를 확보
• 과거 사용된 기억을 고려하면서 더 중요한 정보를 오래 기억할 수 있는 sticky memory 기법 적용
• 실험을 통해 개선됨을 증명